These are the decimal numbers of Phi - a Golden ratio number, which is 0.618033988749894848204586... The precision of number used here is 1000 digits. To see a Golden ratio description, click here.
Use the sliders at the top of the page to zoom onto decimals. To see the decimals in ratio 1:1 click here. To enjoy the interaction fun, try also this preset 1 and preset 2, or try a random values.
CLOSE
is a ratio of circa 62 to 38.
It occures in nature frequently.
To be precise, Golden ratio is
1.618033988749894848204586834365638117720309179805762862135448622705260462818902449707207204189391137484754088075386891752126633862223536931793180060766726354433389086595939582905638322661319928290267880675208766892501711696207032221043216269548626296313614438149758701220340805887954454749246185695364864449241044320771344947049565846788509874339442212544877066478091588460749988712400765217057517978....
...and it continues up to infinty. In following examples we will use just value 1.62 or 1.618.
It’s commonly denoted as Greek letter Phi (φ).
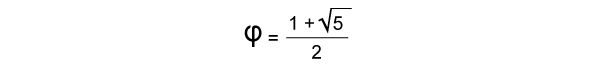
If you want to get following image, where it is stated that ratio of inside rectangles is preserved ...
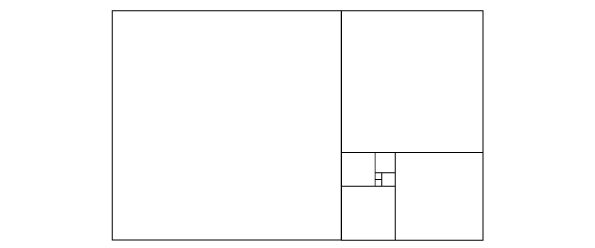
... thus following spiral, the Golden spiral ...

... draw an equilateral square, ...
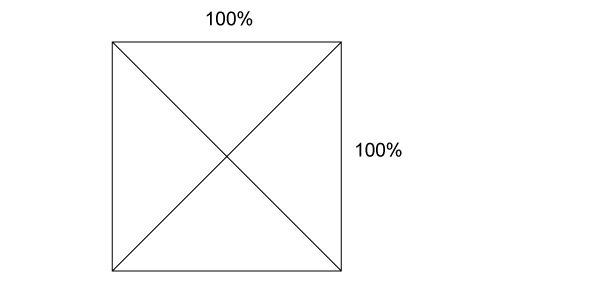
... and multiply the width using such value “X”, so that on the right we will get a rectangle with the same width to height ratio as parent / original / covering rectangle:
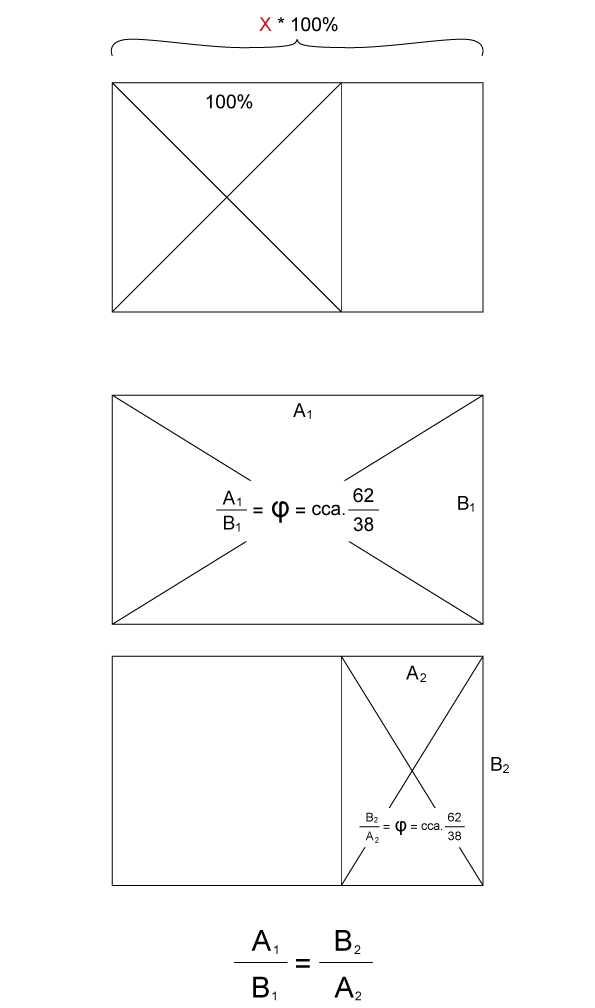
The searched value “X” is 1.618033988...., the Golden ratio, cca. 1.6.
Then, we can continue to do the same procedure - to draw an equilateral square inside the space left, ...
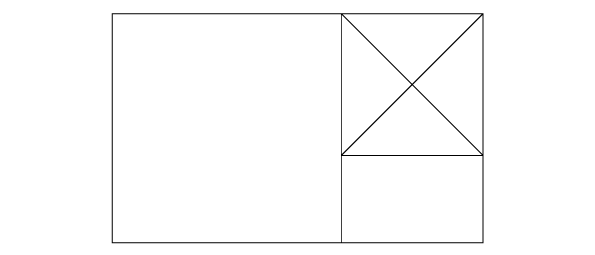
... and the space left this time will be in the same ratio as two parent / previous / containing rectangles.
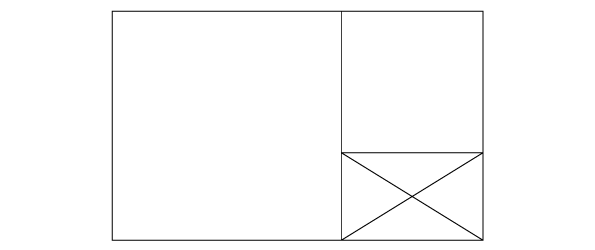
After repeatring the same procedure of inscribibg squares, at the end, you will get following picture:
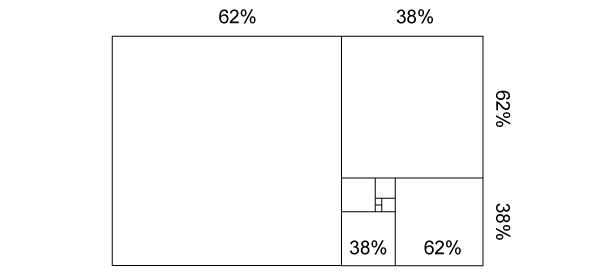
where the Golden spiral appears:

This spiral is special, because the ratio repeats in it.

It’s a logarithmic spiral whose growth factor is cca. 1.618, the Golden ratio.
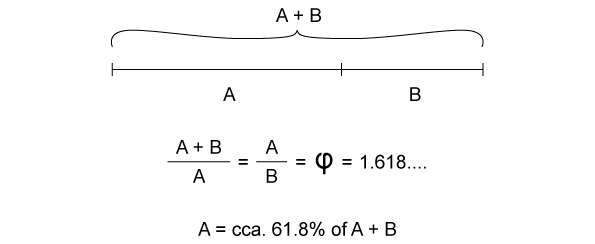
If we draw a line with a length of Golden ratio 1.618 and mark on it value 1, ...

... and mark the line using percentages, ...

... the found percentage value X is 61.8033....% and the number covers exactly the same digits as are the digits those we can find in Golden ratio 1.618033....
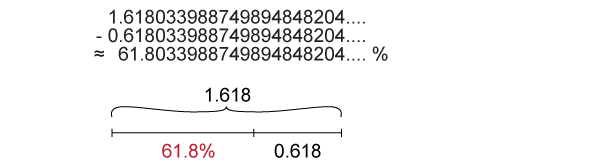

Some examples of Golden ratio:
https://www.csus.edu/indiv/m/mirzaagham/math1/SQ5.pdf
https://gizmodo.com/15-uncanny-examples-of-the-golden-ratio-in-nature-5985588
Wikipedia:
https://en.wikipedia.org/wiki/Golden_ratio
Golden ratio with 50,000 decimals:
https://www2.cs.arizona.edu/icon/oddsends/phi.htm

An example of Golden ratio
using the Great Red Spot (the eye) of Jupiter.
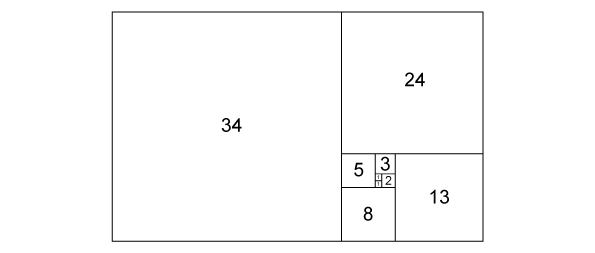
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ... (each number is the sum of the two preceding ones) could be interpreted using Golden ratio too: each side length is a successive Fibonacci number. Fibonacci sequence appear in nature frequently.